Inverse Transform Sampling

The motivation for this blog was a leetcode problem (Generate Random Point in a Circle) I was solving recently. Since this problem was labelled as medium difficulty, I did not have much expectations going into it.

The problem statement is simply asking to generate a random point inside a circle of given radius and center that follows uniform distribution.(Doesn't seem that bad?)

I knew that C++ allows you to generate a random double in the range $[0,1]$ that follows uniform distribution. Let's call this distribution $U$.

Now transforming this distribution to follow the constraints of a given circle felt like a challenge.

Afer some thought, I was struggling to obtain a simple algebraic transformation of $U$ to fit under the constraints of a circle. I could scale the points to fit within a square with the center $(x_0,y_0)$ and keep generating a random point until it fits in the circle.

The probability of a random point generated using this methodology to not fit within a circle:

$$P(\text{point in circle of radius r}) = \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4} \approx 0.785$$

Since, the probability of success of a point follows a geometric distribution, we can determine the expected number of trials:

$$E(X) = \sum_{n = 0}^{\infty} n\cdot p(1-p)^{n - 1} = 1 + (1-p) + (1-p)^2 + ... = \frac{1}{p}$$

Hence, the expected number of guesses in our case:

$$E(X) = \frac{1}{\frac{\pi}{4}} \approx 1.273$$

So it will take us about 1-2 tries on average to generate a point which first the bounds of our circle. I could use this as a possible solution to the problem and but the worst case was still technically infinite time! There is a chance of our first $10^5$ guesses to be incorrect in a row (although the probability of that event is negligible).

I tried to play around with the points generated and different transformations but it lead me to no success. It had already been longer than I have spent on any other leetcode medium problem and I was ready to give up.

Fortunately, that's when I remember the existence of polar coordinates!

All of my computations have been in the cartesian coordinate system but I realized the parameters to a polar coordinate fit the requirements for this problem quite well. The only two parameters required are the radius and the angle the coordinate makes with the X-axis.

Therefore, I just need two uniform distributions, $R$ and $\theta$ such that:

$$r \sim R \in [0,r_0], \theta \sim \mathcal{\theta} \in [0,2\pi]$$

From here, the solution was quite simple. I simply had to generate a radius and an angle in the given bounds and convert the polar coordinates to cartesian. A simple 3 line python solution and I could see the light at the end of the tunnel!

class Solution:

    def __init__(self, radius: float, x_center: float, y_center: float):
        self.radius = radius
        self.x = x_center
        self.y = y_center
    def randPoint(self) -> List[float]:
        r = random.random()
        theta = random.random()*2*math.pi
        return [self.x+r*math.cos(theta),self.y+r*math.sin(theta)]

And with this solution I got hit with a WA on the last testcase...

I mean what could go wrong?! I know that any point generated fits the bounds of the given circle, so why was I getting Wrong Answer?

After some digging and venting, I realized the random point generation might not follow uniform distribution. It is pretty difficult to validate the distribution quickly (since its generated randomly!), so I decided to visualize the point generation.

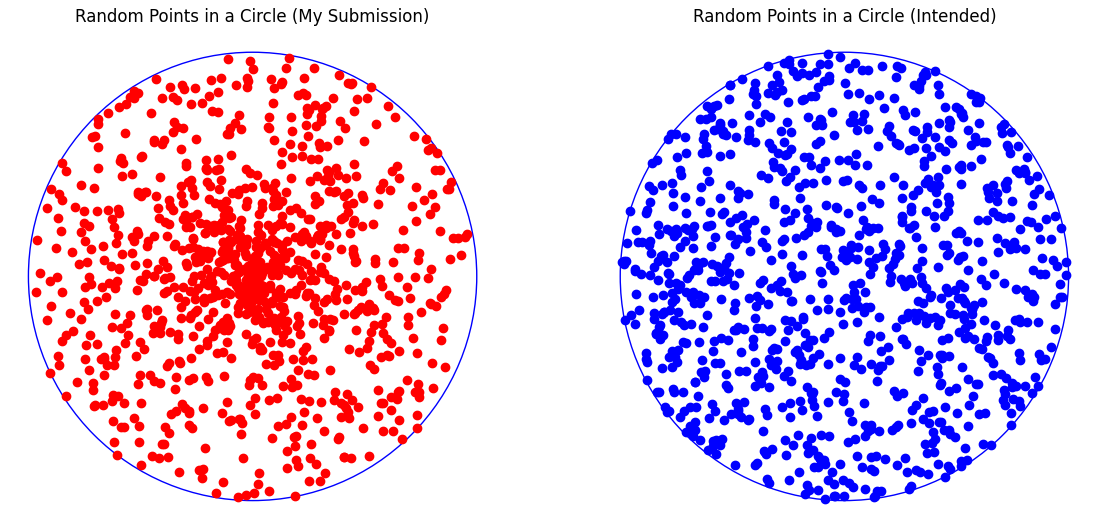
Ah! This was all I needed to confirm my suspicion. My function was not generating points uniformly. For some reason, there was a higher probability of points being generated towards the center of the circle which caused the WA.

But why are my points not uniformly generated? The radius and the angle $\theta$ are both uniformly generated, so I would expect the points to follow a uniform distribution as well.

I realized that our radius is uniformly distributed in the $[0,r_0]$ which means the probability of a random radius variable is constant. However, the area of the circle grows with the increase in the radius $R$. Currently, the expected number of points for a small radius $r_s$ is equal to the expected number of points for a large radius $r_L$. This resulted in more points concentrated towards the center (lower values of $r$) compared to the edges of the circles.

This implies that the Probability Density Function (PDF) for the random variable $R$ must grow linearly w.r.t to the radius.

$$P(R = r) = mr$$

Since, $P(R = r)$ is a valid PDF:

$$\int_{0}^{r_0} mx dx = 1 \rightarrow m = \frac{2}{r_0^2}$$

And our CDF for the radius (R) will be:

$$P(R \leq r) = \int_{0}^{r_0} \frac{2r}{R^2} = \frac{r^2}{r_0^2}$$

Now, that leaves us with generating random variable $R$ that follows the CDF $P(R \leq r)$. However, computers are only able to generate random variable over standard uniform distribution $U$ and not for a custom CDF.

This idea of computer generation for random variables immediately reminded of a concept we learned in STAT 230 at UW!

It is a technique called Inverse Transform Sampling (The title of this blog!). Basically, this technique states that if $F$ is an arbitrary CDF and $U$ is uniform on $[0,1]$ then

$$X = F^{-1} (U)$$

has the CDF $F(x)$ The proof is evident from:

$$P(X \leq x) = P(F^{-1}(U) \leq x) \\ P(U \leq F(x)) = F(x)$$ $$P(X \leq x) = F(x)$$

This made things a lot simpler since, the inverse of CDF in our case was easy to determine:

$$F^{-1} (U) = R \sqrt{U}$$

Therefore, all I had to was use this equation to determine the randomly generated radius.

r = self.radius*math.sqrt(random.random())

Turns out this was all I needed to pass the question!

Looking back, All the mathematical research I had to do to solve a leetcode problem was might have been an overkill but it was definitely worth its time. I guess I should pay more attention to my courses since the concepts I learn might actually be useful some day.